Die (zu) komplexe Frage
nach der optimalen Kurbellänge
(Achtung: auf dieser Seite wird in recht länglicher Weise ihre
letztlich sehr begrenzte Nützlichkeit erörtert)
Modell
und Analyse
Modell:
Betrachtet man den Fahrradantrieb als Wirkungskette einzelner
Mechanismen mit Teilwirkungsgradfunktionen so bildet deren Produkt
den Gesamtwirkungsgrad, welchen zu maximieren das
Ziel ist.
Diese Wirkungskette
enthielte (zumindest) folgende Teilbereiche (das Rad wird
hierbei
vom Hinterrad her
aufgezäumt):
0. "Äußere Verluste" Reibung im Fahrrad-Antrieb
Durch Reibung entstehen Verluste im mechanischen
Übertragungswirkungsgrad des gesamten Fahrradantriebes
(Pedale-Kettenrad-Ritzel-Hinterrad-Strasse)
Diese Verluste (Reibung) sind bei
guten Komponenten ausgesprochen gering und treten außerdem
unabhängig von
den interessierenden
biomechanischen Verlusten auf. *)0
1. Nicht tangentiale Kraft am
Pedal
Die mech. Leistung am Kettenrad ist das Produkt von
Trittfrequenz x Kurbellänge x tangentiale Tretkraft
*1)
Kraft
aus
Muskelanspannung zu erzeugen, bedeutet für einen Muskel immer bereits
Energieumsatz also
(chem.)
Arbeit.
Jedoch nur der in "Drehrichtung" wirkende Pedalkraftanteil
leistet als Antriebskraft die mechanische Arbeit, während die
andere
Kraftkomponenten (vor allem in Richtung des
Kurbelarms) lediglich als statische Anspannung den Muskel anheizt. Die Fähigkeit, einen
möglichst großen Teil der ausgeübten Pedalkraft (dynamisch) in Richtung des
drehenden Pedals (tangential) einwirken zu lassen, ist abhängig
von
: Leistung,
Trittfrequenz, Kurbellänge, Muskelaufbau,...
2. Innere
Reibung in Muskeln und Gelenken
ist zwar hoffentlich nur gering,
stellt aber ebenfalls einen unvermeidlichen Verlustfaktor dar.
Ein
wesentlicher Anteil entsteht dadurch,
daß verschiedene Muskeln in der Gesamtbewegung nicht ideal abgestimmt
sondern gegeneinander arbeiten. Die Minimierung kontraproduktiver
Muskeltätigkeit gehört wesentlich zum Training des sog. "runden Tritts".
Auch
die
inneren Reibungsverluste im Bein sind abhängig
von: Leistung,
Trittfrequenz, Kurbellänge, Muskelaufbau, Sitzposition, Fußtechnik...
3.
Stoffwechseleffizienz im Muskelapparat
Zum Stoffwechsel gehört die chem. Energiezufuhr (z.B. Zucker) und
Abtransport der Stoffwechselprodukte (z.B. Milchsäure).
Ca. 7 am Bein ansetzende Muskeln leisten (abhängig von Sitzposition, Bewegungsablauf, ...) die Antriebsarbeit (siehe z.B. hier).
Für eine hohe Leistungsabgabe der Muskeln über lange Zeit muß (auch unter der
Annahme immer ausreichenden Blutzuckerspiegels) kontinuierlich deren
genügend hohe Durchblutung sichergestellt sein.
Können Stoffwechselprodukte (wie
Milchsäure) nicht schnell genug abgeführt werden, kommt es zur
Übersäuerung und die Muskelleistung fällt ab. Sehr wichtig für die hohe
Durchblutung - auch der zentralen Muskelbereiche - ist ein Wechselspiel von
Anspannung und (möglichst vollständiger!) Entspannung. *)2
Desweiteren haben die Muskeln (abhängig von ihrer[in Grenzen
adaptierbaren] Struktur: kurze/lange Fasern) bei bestimmten
Kontraktionsgraden ihre besten Wirkungsgrade.
Deshalb sind
auch diese Prozesse wieder deutlich abhängig
von: Fahrertyp(Größe,...), Leistung,
Trittfrequenz, Kurbellänge, Sitzposition, Muskelaufbau, Fußtechnik...
Zielfunktionen
Zielfunktion:
max. Leistungdurchsatz auf Dauer
Radprofis haben so
hervorragend trainierte Beinmuskeln, daß Ihre Dauerleistung wesentlich
durch die (schwerer zu steigernde) Leistung des Herzmuskels sowie die
Atmung begrenzt wird. Unter Beachtung dieser Grenzen wird gewöhnlich
physiologisch der maximale Leistungsdurchsatz angestrebt. Über
eine längere Zeit kann dieser nur ohne nennenswerte Übersäuerung, d.h.
bei perfektem
Stoffwechsel aufrechterhalten werden kann. Dies ist z.B. besonders
relevant für lange Bergetappen oder Einzelzeitfahren, wenn jeder nur für sich allein kämpfen muß (ohne
Windschatten). Veränderliche Sitzpositionen bzw.
Wiegetrittanteile
ändern jeweils die Randbedingungen u.U. deutlich.
Zwischen Trittfrequenz und Atmung sind zumindest
im
Wiegetritt engere Kopplungen zu vermuten (Trittfrequenz Vielfaches der
Atmung)
Möglicherweise bestehen auch optimierte
Kopplungen zwischen Trittfrequenz und Herzschlag(?)
Zielfunktion:
max. Kurzzeitleistung
Dort
wo Radrennen im
Schlußsprint (z.B. aus dem Windschatten des Feldes heraus) gewonnen
werden,
also die kurzzeitige und abschließende Maximalleistung rennentscheidend
ist, ändern sich die Randbedingungen stark, da eine Übersäuerung der
Beinmuskulatur im Moment der Zieldurchfahrt kein Nachteil mehr für den
Sieger darstellt.
Dies hat sicherlich Auswirkungen auf die Lage
biomechanischer Optima.
Zielfunktion:
streckenbezogener Energiebedarf
Wiederum
eine andere Stoffwechsel-Zielfunktion ergibt sich, wenn jemand mit
relativ geringem Futterdurchsatz (d.h. energie- geld- und CO2 sparend :)
durch die weite Welt
radeln will (streckenbezogener Energieverbrauch). Hier ist ja nicht
mehr maximaler Leistungsdurchsatz des Sportlers
gefragt sondern tatsächlich der Gesamtwirkungsgrad, welcher bei
deutlich geringerem Energieverbrauch (und z.B. auch bei geringerer
Trittfrequenz) liegen dürfte.
Das Training auf eine bestimmte
Zielfunktion hin
hat wiederum umbauende und anpassende Rückwirkungen auf den Muskelaufbau.
Für die
Kurbellänge gibt es außerdem auch noch hart begrenzende Körpermaße.
Wenn z.B.
in Rennradposition die Oberschenkel beim Treten an den
Hängebauch stoßen, muß entweder die Kurbel verkürzt oder der
Lenker höher
oder Sitzposition nach vorn genommen (oder der Bauch verschlankt)
werden.
FAZIT: (viel)
zu komplex für geschlossene Gesamtanalyse!
Die vorstehend aufgezählten körperbezogenen Faktoren
- sind sämtlich
(aber
verschieden) abhängig
von der Kurbellänge und den weiteren
Parametern!
-
sind erheblich von
gewählten
Randbedinungen
und der
aktuellen Adaption
des Fahrers abhängig
-
sind tatsächlich nicht unabhängig sondern untereinander in
komplizierter Weise verkoppelt
- hängen von
der konkreten
Zielfunktion ab
Eine
geschlossene theoretische Analyse wird damit kaum
vorstellbar.
Und eine
fundierte experimentelle Untersuchung müßte aufgrund der vielen
einzugrenzenden Randbedingungen und deren Rückwirkung auf den Fahrer
zumindest extrem(!!) aufwändig und damit auch extrem teuer sein.
Im überschaubaren
Experimentreihen können
allenfalls Teilfragestellungen mit stark einschränkenden
Randbedinungen geklärt werden, wie z.B.:
- Wie ist die optimale
Kurbellänge für den Radfahrer F mit (den Körpermaßen XY) im
Adaptionszustand A und Trainingszustand Z nach Ausgeruhtheit R auf
einem Ergometer in Sitzpositon S bei konstanter Leistungsabgabe P
über 60
min?
- Wie ändert sich dies tendenziell, wenn die Leistungsabgabe nun auf P2
angehoben wird (z.B. Bergfahrt)?
- Wie ändert sich dies tendenziell, wenn der Fahrer länger (oder
periodisch) in den
Wiegetritt geht?
praktikabler
AUSWEG:
linearer
Ansatz - kalibriert am Spitzensport
Das Megaexperiment
Nachdem
die Erwartungen an eine kausale Durchdringung und analytisches
Verständnis zurückgestellt sind, können wir uns dennoch, an die
Auswertung des einzigen wirklichen Großexperimentes
heranmachen. Dieses war zwar nicht vorrangig als
Kurbelexperiment geplant,
jedoch führt der enorme Gesamtaufwand mit dem es
betrieben wurde (und wird) auch unter geringen Annahmen automatisch zu
einigen verwertbaren Ergebnissen. Denn in der Weltspitze des Radsports
ist die Leistungsdichte inzwischen so eng, daß Fahrer
mit erheblich suboptimaler ergonomische Anpassung
(hochwahrscheinlich) automatisch
deutlich nach hinten befördert werden. Man kann daher mit guter
Wahrscheinlichkeit
annehmen, daß kaum einer der Spitzenradler fern seiner optimalen
Kurbellänge fährt (Profis die das tun, sind zwar immer noch
Supersportler aber
eben kaum mehr die Spitzenradler). Mag die
Versuchsführung selbst
chaotisch sein- der pure MegaAufwand, den kein Forschungsinstitut
jemals leisten könnte oder finanziert bekäme, wirft (quasi nebenbei)
das vermutlich bestfundierte Ergebnis statistisch mit ab.
Wertet man dieses
Megaexperiment des Weltradsportes nach Kurbellängen statistisch aus,
dann sind die Daten desto wertvoller, je höher die Leistungsdichte an
der Spitze im betrachteten Zeitraum war, vermutlich also mit fortschreitender Zeit.
Ältere
Daten wären dementsrechend schwächer zu wichten.
Die
Ergebnisse, die der Spitzenradsport liefert, können prinzipiell jeweils
auch
Hinweise zur tendenziellen Abhängigkeit optimaler Kurbellänge für die
verschiendenen Disziplinen liefern, in denen die Leistungen
erbracht wurden (Einzelzeitfahren, Bergetappen, Schlußsprints,...).
Weshalb linearer Ansatz?
Sofern man (überhaupt) über Kurbellänge spricht,
zieht man also deren Veränderlichkeit in Betracht. Der
Gedanke,
daß ein existierendes Optimum mit Körperlängenmaßen des Fahrers
proportional skaliert, ist dann (nach dem der "Einheitskurbel") der
einfachste (und wohl
auch naturgemäß naheliegend.)
Desweiteren wird
man für verschieden größe (und ähnlich proportionierte) Fahrer jeweils
optimale ergonomische Bedingungen zunächst bei ähnlicher Fahrweise,
d.h. gleichen Beugungswinkeln
der Gelenke (Hüfte, Knie, Fuß) suchen. Dies führt zur
"in erster
Näherung" proportionalen Abhängigkeit.*)4
Betrachtet man die
angeführten Beugungswikel, wird klar, daß die Beinlänge eine noch
bessere Bezugsgröße ist als die (meist sofort bekannte)
Gesamtkörperlänge.
Bei
noch genauerem Hinsehen könnte man Oberschenkellänge (evtl.
auch den Fuß) stärker
wichten als den Unterschenkel.
Es ist nicht erkennbar, warum
und welche anderen Einflußfaktoren die dominante Führung des
proportionalen Trends
übertreffen könnten.
Korrekturen "von höherer Ordnung" werden zwar prinzipiell existieren, diese werden
aber bei nur rel. geringen Abweichungen vom
Mittelwert (+/-10% entspricht +/-18cm Körpergröße) auch nur sehr
geringen
Einfluß haben.
Konstatiert man aus den vorliegenden Fahrer-Kurbel-Daten
naheliegenderweise stattdessen lieber eine deutliche "individuelle Streuung" von
(Standardabweichung ca.)
+/- 5 mm Kurbellänge, so darf man annehmen, daß sämtliche Korrekturen
höherer Ordnung von diesen +/- 5mm Individualität überdeckt werden.
Als ein Element für eine Korrektur höherer Ordnung ist z.B. ein Körpermasseindex anzunehmen, welcher auf die tendenzielle
Nichtproportionalität
längerer gegenüber kürzeren Menschen abzielt (länger => eher
dünn).
*4) Sofern eine solche körpermassenbezogene Korrektur jedoch erkannt
und ihre
Richtung und Betrag beziffert werden können, dann wäre es allerdings wieder deutlich
sinnvoller, sie _direkt_ (also nicht implizit als Tendenz über die
Körperlänge) zu integrieren, zumal ja die Körpermasse eine besonders leicht
zu
bestimmende (neben der Körperlänge meist sogar schon bekannte) Größe
ist.
Für verschiedene Stufen der Betrachtung erhält man Kurbelformeln der
folgenden Form:
0. Näherung (konstante Näherung)
Einheitskurbel. D.h. für alle Menschen und Einsatzzwecke ist (fast)
einheitliche Kurbellänge von (z.B.) ca. 175 mm ausreichend geeignet.
Einheitskurbellänge := 175mm !
1. Näherung bezogen auf Körperlängenmaße (linear (proportional) zu
einer Körperlänge)
1.a) auf Körperlhöhe bezogen
z.B.: Kurbellänge = 10% Körperhöhe
(+/- 10mm individuell)
1.b) auf Beinlänge bezogen (z.B. als Schritthöhe gemessen)
z.B.: Kurbellänge = 20,5% Schritthöhe
(+/- 10mm individuell)
1.c) auf Oberschenkel bezogen
...
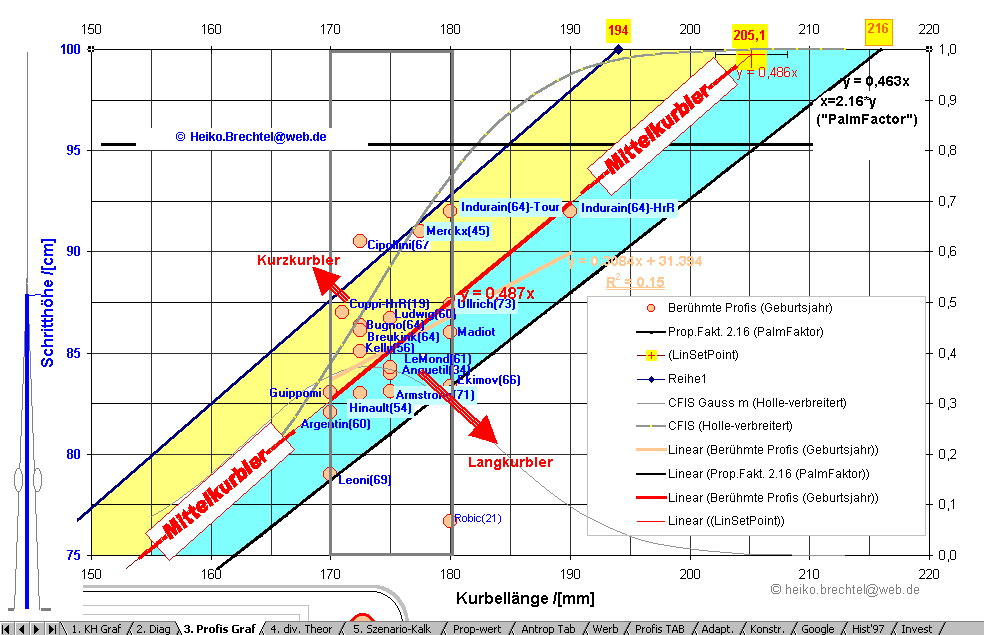
Der
bei 1.b) angegebene Wert von 20,5% Schritthöhe ergibt sich
für Spitzensportler. Für Hobbyfahrer oder Reiseradler weicht
möglicherweise der anzuratende Wert bei ab (z.B.19,5% oder 21,5%).
Nicht betroffen davon ist jedoch die Annahme von der
Proportionalität der optimalen Kurbellänge zur der Länge des Fahrers.
(Diese
läßt sich übrigens leicht überprüfen, indem man die gemessene Länge
eines gegebenen Fahrers durch Dehnung des Längenmaßstabes verkürzt.
Diese Dehnung des Längenmaßstabes kann die Auswahl der
optimalen Kurbel natürlich nicht beeinflussen. Dennoch wird man bei
Überprüfung der Kurbel mit dem nunmehr ja gedehnten Längenmaßstab
feststellen, daß sich das Längenmaß der optimalen Kurbel um genau
denselben Prozentsatz verkleinert hat wie das des Fahrers. Genau dies
war bei Annahme von Proportionalität auch zu erwarten q.e.d.:)
Und hier noch eine kleine
Verschwörungstheorie...
Als interessant könnte man es deuten, daß die
Streuung der Körpergrößen (Standardabweichung in %) in der
(internationalen)
Radweltspitze (sogar) signifikant geringer ist, als Streuung
innerhalb einer nationalen Population (z.B. Deutsche).
Wenn es nur ein eng begrenztes Kurbelspektrum gäbe, dann
könnte man voranstehenden Sachverhalt daraus erklären, daß ein
marktgängiges "Kurbellängenfenster" sich auf ein eingeengtes "Faherfenster" (im
Hochleistungsbereich) abbildet.
Tatsächlich ist bisher (für
den Breitensport, aus dem sich ja letztlich auch die Spitzenkader erst
einmal rekrutieren müssen) das verfügbare Kurbelspektrum weitgehend
auf ein
Fenster von 170-180mm beschränkt. Dies hilft nun möglicherweise
auch,
das Körperlängenfenster an der Weltspitze beisammen zu halten.
(Es sind allerdings auch andere Erklärunggründe für den
Effekt möglich und vielleicht auch maßgeblicher.)
* * *
*)0
Zu den aus biomechanischer Sicht "äußeren Verlustfaktoren" zählt
natürlich auch der Luftwiderstand, dessen Überwindung auf ebener Stecke
fast alle Anstrengung des gut ausgerüsteten Radfahrers gilt. Er ist
abhängig von der Sitzposition und damit mit der Biomechanik verkettet.
Aus Kurbelverlängerung (an einem gegebenen Fahrrad) ergibt sich z.B. eine
etwas geringere Sitzposition, was den Luftwiderstand geringfügig
vermindern kann.
*1)
Häufig wird eine einzelne der drei Größen (Drehzahl, Kurbellänge,
Pedalkraft) herausgelöst und dann separat (oder zumindest
sehr bevorzugt) bewertet.
z.B.:
"Mit einer langeren Kurbel ist man
viel besser am Berg, wegen der längeren Hebel!"
oder
"Der
Lance hat es alles über die hohe Drehzahl gemacht -
so siegte
er."
Eine separate Betrachtung von Kurbellänge oder Drehzahl
oder Pedalkraft ist aber fast immer unsachgemäß, weil alle
drei Größen zunächst in
ähnlicher Weise in die Leistung eingehen und die Vergrößerung eines
der drei Werte tendenziell stets zu Lasten (mindestens) eines anderen
geht.
So
verringert sich bei Kurbelverlängerung tendenziell die Drehzahl. Erst
dann wenn der Drehzahlabfall (prozentual) geringer ausfällt als die
Kurbelverlängerung (oder sich durch letztere die (tangentiale)
Einleitung der Pedalkraft
verbessert), dann wird die Leistung steigen. Möglichkeit und
Notwendigkeit von Adaption verwischen einfache Kausalitäten weiter.
Und so konnte Lance
Armstrong wohl nur deshalb siegen, weil er gleichzeitig (!)
-
mit hoher Drehzahl und (obendrein)
- an relativ langer Kurbel (für seine Körpergröße
=> ca. 21% Beinlänge=Langkurbler)
- immer noch (und ausdauernd) hohe
(tangentiale) Pedalkräfte einkoppeln konnte.
Daß er zu all dem in der Lage war, ermöglichte natürlich nur seine überlegene Verfassung.
Sehr stark zu vermuten bleibt aber sehr wohl, daß sich alle biomechanischen
Parameter sehr nahe an den Optimalwerten für L.A. befanden.
Was die "Hardware" berifft, heißt dies vor allem: gesamte Sitzposition und
Kurbellänge.
Und stets (nicht nur bei der Kurbellänge) ist auch der Bezug zur
konkreten Körpergröße mit im Auge zu behalten.
Eine Giraffe kann auch recht schnell laufen, obwohl sie nie die
Schrittfrequenz und Beschleunigung schneller Gazellen erreichen kann.
In ähnlicher Weise ist die Bewegungsabfolge langer Menschen
tendenziell langsamer.
Größere und damit häufig schwerere Menschen können hingegen tendenziell auch mehr Pedalkraft ausüben.
Was für Jan kurz ist, kann für Lance zu lang sein usw...
*2)
Auch dies ist ein wesentlicher Bestandteil des idealen,
oder "runden Tritts". Damit wird auch klar, daß *runder Tritt* nicht
die möglichst konstante Krafteinleitung auf dem gesamten
Kurbelumfang bedeutet (was eine höhere permanente Anspannung zur Folge
hätte) sondern neben möglichst hohen Tangentialkomponenten
der Pedalierkräfte sehr wesentlich auch die effiziente periodische
Relaxierung aller wichtigen Muskelgruppen beinhaltet, um deren
Stoffwechsel zu befördern.
*3)
klärend
sei angemerkt, daß z.B. die Laufradgröße keine relevante Größe
für
die Betrachtung ist - ein größerer Fahrer mithin kein größeres Laufrad
benötigt.
Relevant für die biomechanischen Betrachtungen
sind ausschließlich diejenigen Parameter, die unmittelbar Position und
Bewegung des Fahrers beeinflussen.
*4)
Auch nichtproportionale lineare Kurbelformeln sind vorgeschlagen worden
(z.B. Genzling 1986/88 "Im Rennsattel") jedoch ohne nachvollziebare
Begründung.
Aus solchen Empfehlungen scheint mehr das (vielleicht unbewußte) Motiv einer
möglichst "gerechten" Verteilung des (damals) in den Läden vorhandenen
Kurbelangebotes von 170mm-175mm (bzw. für "Experten" auch bis 180mm) auf
die Radfahrergemeinde zu sprechen.
notiert am 29.9.07
